Crazy Comparison – Sony NEX-5n and Leica M9 Image Quality!
Ok everyone, here it is! You know I have been shooting the Sony NEX-5n with my Leica 50 Lux ASPH via an adapter but I also have been shooting with my M9P as well. You all know I LOVE MY LEICA M9P and I will be the first to say it right now, the Sony NEX-5n feels like a toy in comparison when held in the hand. There is nothing quite like the feel of the M9 and this “Crazy Comparison” will be based ONLY on image quality of the out of camera JPEGS. Why no RAW? Well, there is no real support for the NEX-5n RAW files yet and I only use Lightroom and Photoshop these days.
Also, all of us M9 users know that it’s weak link is its JPEG output and it shines with RAW, so this comparison is basically just to give an idea of what the output of both cameras are with JPEGS and to also show the difference between a full frame sensor and crop sensor. The M9 beats the NEX-5n in every way, make no mistake! The body, the build, the simplicity, the control, and the full frame sensor takes advantage of the glass and exploits its full qualities.
Keep in mind though, for all of the differences in build, size, and control the NEX-5n is 10X less expensive and the image output is not that far off at all from the M9. When there is full RAW support I expect the same thing really as the 5n’s JPEG output is VERY good so its RAW files will be even better.
So, can the 5n be called the poor mans Leica M9? In my opinion NO, because it is a totally different kind of camera. The M9 is a rangefinder and you shoot with it in a totally different style. So the NEX-5n will never give you the RF experience. The NEX-7 will bring y ou a step closer with a slightly larger body, more dials for manual controls, built in EVF, etc and in fact, The NEX-7 will be a game changer, mark my words! I feel something like a NEX-7 with Leica glass with not only be a joy to shoot, but also give better quality than an M8 with the same lenses. But, the 7 will also be a different experience than shooting an RF and if you are an RF person, and love to shoot an RF neither of the new Sonys will cut it.
Me, I see the 5n or even better the NEX-7 as a GREAT backup to the M8 or M9 and for those who do not want the “RF” experience, the 5n and the upcoming 7 will be fantastic options for those looking for a high quality body for their Leica glass. The Ricoh GXR is also coming but I feel the 7 will give a better user experience and even output though the GXR may pump out super sharp files due to lack of AA filter. I’m liking what I am seeing so far from the NEX and still am looking forward to the 7.
The quality in the 5n is there, and shooting with the EVF is quick and easy. See the full size comparison shots below:
1st up: The M9P and 50 Summilux ASPH at 1.4 – Out of camera JPEG, AWB. Click image for full size file.
–
2nd: The NEX-5n and 50 Summilux ASPH at 1.4 – out of camera JPEG – AWB – Click image for full size
The shot below is from the M9P, again with the 50 Summilux ASPH.
–
and the 5n and Summilux
and one for fun with different lenses – Leica M9P and 50 SUMMITAR at f/2
and the NEX-5n with the 50 Lux at 1.4
–
Once again, the M9P is first – straight JPEG from camera – 50 1.4 at 1.4
–
and the 5n with 50 lux at 1.4
another one…1st up, Leica M9 and 50 Lux at 1.4
and the 5n with the lux at 1.4
[ad#Adsense Blog Sq Embed Image]

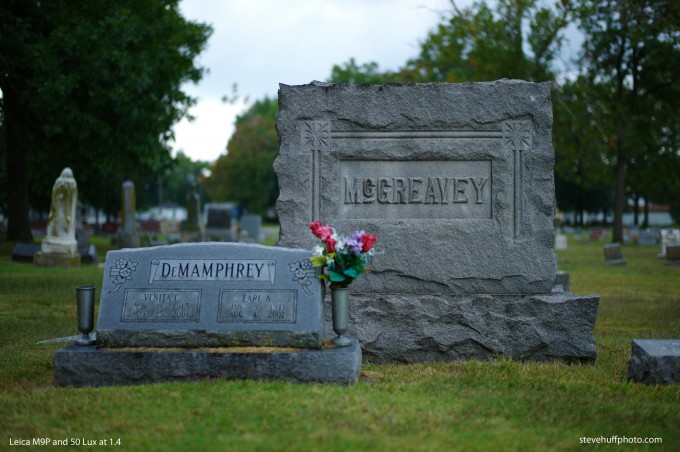
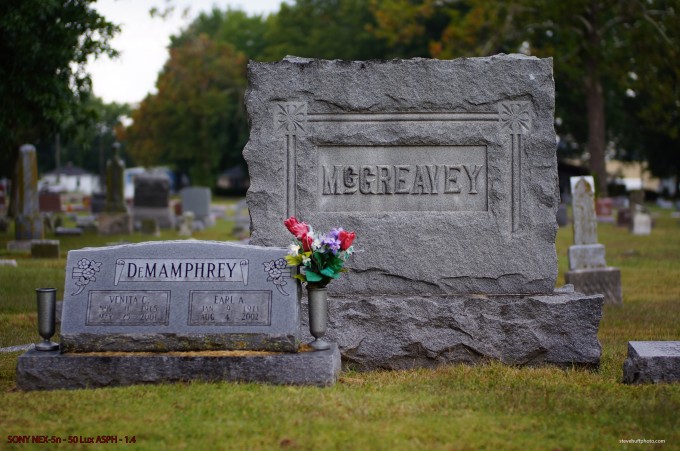









any word on Alpa 35mm resurrection ?
Thank Steve, i like the sharpe of nex 5N better, now i own nex 5n, i am happy with the image quality^_^
thanks Steve
So , how can I check the raw files from both cameras? Any links for downloads?
Or it’s some kind of secret… to keep leica users secure
I can not offer RAW files due to bandwidth and what it would cost me to offer these for download to hundreds of thousands of people. I’ll say it, the 5n ROCKS with that 50 Lux at a MUCH cheaper cost.
I think we take the list of 10 features that M9 lacks too seriously. It reads more like a tease or troll than serious complaint.
Eric we are comparing picture quality, not the features. Btw M9 doesn’t do live preview, that’s why it’s a rangefinder, it calculates the range mechanically and optically, adjusted manually with precision.
Regarding the expensive M9 vs the relatively cheap NEX-5N / NEX-7:
People should put the Leica M9 in perspective and consider its shortcomings
—————————————————————————————————————
1. 2.5″ fixed non-articulating LCD, 320×240 resolution. The LCD is too small, has a very low resolution and is fixed in place. That’s probably why all M9 users need the ViewFinder. The LCD is simply terrible and non-usable at all for judging composition.
2. No Auto-focus
3. No video recording capability
4. No HDMI out
5. No Wireless option and no remote
6. No SDXC support
7. No built-in flash
8. No Timelapse recording
9. No GPS
10. ISO up to 2500 only. Leica tried to make up for this by making very fast lenses, but as you all know, they are very expensive. Don’t even consider attaching a lens that has an aperture of f/2.8 or worse. F/2.0 is the bare minimum that’s recommended if you need to shoot in low-light situations.
Yeah, but if I can afford M9, I will buy M9 in a heart beat. Its PQ has such a depth I don’t see in any camera. I think its lenses contribute greatly to this (I really like Leica 28-90mm zoom on 5D Mk2). So if NEX PQ is close to M9, that’s wonderful news. I can’t wait until NEX has full-frame.
1. you are right, LCD is crap
2. it’s a rangefinder.
3. video would be cool
4. who cares
5. who cares about wireless. remote would be nice
6. SDXC so I can lose my 2TB card with 10,000 photos. meh.
7. who uses flash? who uses built-in flash? LOL. got my iphone if I want to take crappy built in flash photos
8. LOL
9. I have my iphone for gimmicks. My 5Dii didn’t have this either and couldn’t care less
10. Leica tried to make up for the ISO rating by making fast lenses? LOL! They had fast lenses long before the M9 and M8 came along. Don’t fix a f/2.8 lens to the camera? Am I only shooting low-light or perhaps is there times during the day when the light is bright?
when SD15 was released with half of the weakness above, ppl rated it lowly. When leica did the same and double the “not so updated technology” missing list, its the world best photography tool. Its all just mass mentality really.
What the world should pay attention to is how both SD15 and M9 stop implementing junk features like panaromic handheld, artistic filters, scene modes and all those craps. Keep the controls simple, this is one area the M9 trounces nearly everyone, with the exception of GXR which is the only digital apsc that found the holy-grail layout for UI.
Apart from “autofocus”, “wireless” and “sdxc” the rest of the list above are just fancy gimmicks that adds nothing to the photography experience and more towards mass market of pppl who are clueless on what they want.
Looking at those files, the Sony beats the Leics in a number of aspects, the detail in the images is much much sharper from the Sony, I pefer the OOF rendering on the Sony to the leica, the M9 looks too soft and creamy, while the Nex gives a nice change from super sharp to nice quality Bokeh, unlike the M9 files that look like someone has smudged vasaline on the lens.
If the Nex 7 beats the 5 in terms of detail & resolution then coiupled with it’s supposidly amazing OLED EVF I don’t see any reason for people to invest in an M9 other than for the Kudos of the red dot. The Sony will be clearly the better camera & at the end o the day it’s the images that matter not the style of the camer.
+1
one day steve should do a comparison using Sigma SD15. it wont make money for his site, but everyone can see for sure, how a 4.7 mp can trounce both nex and m9 in DR and sharpness. Oh…there is the SD1…unfortunately way too powerful for today’s layman computer to process the raw files in acceptable time.
> the NEX-5n is 10X less expensive and the image output is not that far off at all from the M9.
I don’t see that looking at your full size example images. There is a lot wrong with the NEX-5n JPEGs at 100% or slightly reduced size. The M9 files actually look quite okay. At reduced size both cameras deliver good enough quality, but so does pretty much any other “serious camera” from the past 10 years or so. Perhaps the NEX does better with native lenses.
Ditto that last comment.
One more thing…
It’s two different sensor sizes, so Steve had to close up for M9 to get the same frame has NEX. The DOF on Leica was thinner than on NEX5n causing more bokeh on M9’s pictures.
These comparisons will be made by someone anyway…
So it is a good and honest approach by Steve, what ever camera we choose to buy or can afford to buy it must feel good in the hand and inspire us to want to get out there…
if it feels like a metallic brick in the hand it probably won’t do much for anyone… regardless of image or cost saving… it is exciting that there is a camera for everyone to be inspired by. Happily we are all different… and yes I do agree that a true comparison for the M9 for its strengths need to be done in RAW but yes it’s good to see what the competition can do… even if it can only be done in jpeg so we all need to keep an open mind…
Oh and remember Steve’s site started with the M8 which could never by any stretch of the imagination be regarded of the best digital 35mm camera at the time. However, it inspired him and that’s what it is all about.
Hi Steve, thank you for the comparison. Nice work, as always!
We can compare image quality, but there’s one thing that Leica always will win for sure… Love. The Leica digital M mimics the old RF film camera, there’s not much pleasure when you pick a AF camera and shoot, Leica M give’s you that feeling that you are creating art.
Another advantage of Leica is the CCD that has a wider dynamic range control in raw. It’s not fair to compare Leica’s jpg with NEX’s one because they NEX has new better jpg processor.
Also the Leica’s jpg is very flat, I mean not sharped, no contrast, no compensation.
There must be a reason for brands like fuji, sony,canon,nikon are trying to mimic Leica feel to their products.
Regards.
-P.B.
People compartmentalizing and quantifying Leica miss the point – the totality of experience.
Undoubtedly there are posers, and Leica does cater to them, much as the new Ferrari’s do,
but that’s the sign of the times, not Leica per se.
The NEX sample images are unbalanced, thin and vague.
Perplexed as to what people are seeing in them.
I know it has been said before-anyways:
Everybody who has ever compared an M9-out of camera JPG with an M9-RAW image knows that the M9 jpg are do not show at all the IQ which can be achieved with raw.
I dont know why you spend so much time on comparing images and then only use jpg.
If there is no software to convert nex raw then using nex jpg and m9 raw would be much more helpful IMO.
The M9 JPG engine may be poor but it still trounces the NEX which obliterates finer details.
Thanks Steve for the comparison. However I don’t think you were crazy to compare the cameras but BRAVE to do so….based on some of the comments.. I love your site and learn something everyday.
Kind Regards to All
Hi Steve
Turns out that this is a great test and the winner is the Leica glass. Thanks for another great article.
Cheers Peter
I’m just saying that you’re not doing Leica any favors by having these “crazy” comparisons.
I would be interested in your advice on how best to deal with the CA. Can you just stop down the lens, or do you need a slower lens?
I don’t understand this debate about cost of camera. It’s totally irrelevant to me. If I can afford M9, I would buy it. The combination of M9 and M-Leica glass is so amazing that I don’t see from other DSLR set up.
I am glad that there is a cheaper alternative, even though it’s not full-frame, that has excellent IQ and lets me use M-glass (which I will save pennies for) and R-glass (which I have).
Once again you’ve proven that the M9 isn’t worth 10 times the cost.
I wan the same thing from my camera something that feels and look like a film camera, i walsy have ready to go out my FM2 or my Rolleiflex but i alwasy cary my Gf1.
I juat waht something small that prints great up to 40x60cm, end of the story, i’m tired of buying and selling gear.
Greg
I agree with those of you that write about film. Film can easily produce wonderful images and often better than anything from digital cameras. But film is not so pratical, because it must be developed and scanned.
I often tell myself to grap the 35Ti or F4 or whateever and shot some more film, but most of the time I just grap my X100 or Canon s95 which I always carry with me, because it is so much easier than handling film.
To a large extent, many M9 users don’t buy for image quality, modern feature set, etc. We bought the M9 because we were happy with manual film cameras, and the M9 is the ONLY digital that duplicates that shooting experience, but avoids the inevitable unavailability of film. I suppose this only appeals to us old folks – but there are a lot of us out there.
New features won’t make me change cameras. I’ll change when my M9 breaks and can’t be repaired. After all, my Leica lenses are all 40 to 60 years old, and are more than capable for my use.
I have an M8.2 and I think it’s OK. However, since I bought a couple of Leica M6 TTLs (.72 and a .85) my M8.2 is collecting dust. The point is that what creates a beautiful photograph is the available light AND a great lens. If you have some of Leica’s great lenses, including the new 35mm Summilux and the 50 Summilux, in my opinion you’ll get great photos using any of Leica’s great film cameras, i.e.,
M6 TTL, M7 or MP. You don’t need to get on the digital merry go round to make great photos. Shoot film! It’s cheap and it’s wonderful. Try Ilford 100 and you’ll be surprised at the black and white photos the great Leica lenses produce. You don’t need an M10. Film cameras excel with the right light, lenses, and filters using good quality film. It’s more fun too!
In order for the NEX5N or 7 to have any impact on Leica’s bottom line, someone who was about to plunk down hard cash on a M9 would have to reconsider and purchase a NEX model instead. I frankly don’t see that happening. If you can actually afford a M9, you can afford a M9 and a NEX – and that is exactly what I’m seeing (people who own M9s are the ones posting all of these comparisons with the NEX cameras, remember?). Not being able to afford a M9 and buying a NEX because you feel it is superior to a M9 does not affect Leica (who had blockbuster financial year – for them – last year). You are not their market. Buying a NEX and then purchasing Leica glass to go on it to prove it is superior to a M9 actually helps Leica, so I don’t really see them upset by any of this.
Judging from some of the comments, buying a NEX will allow you to feel superior to those who own or purchase a M9, so I suppose that reverse-snobbery is a ancillary benefit of the Sony camera. 😉
The situation is no different than it was a few years back when, feature-wise, you could get a much higher spec’d camera than a M8 for about half to 1/3rd of the price (you can follow this trend back several decades – just substitute a Nikon F100 and a Leica M7 for the NEX 7 and M9, etc). That didn’t stop people from buying M8s. The situation will be the same when the M10 is eventually released.
That was a fun comparison.
Next time you might let people guess which camera/lens was used to take each picture, it will be even more fun! Then the following day, you can update the post and reveal the truth…
Leica may get priced out of the camera market soon. The M-9P is too expensive. And, it’s likely that the upcoming M10 will push the $10K limit, creating a tough market for Leica digital SLRs. I went thru this digital scenario with Canon cameras. Every time I bought a new/latest Canon digital camera, I thought I was done spending thousands of dollars on camera bodies…..that is until Canon came our with their latest and greatest digital model. Canon can get away with this scenario since they are selling digital cameras that are in the range of $2K to $6K (for the most part), but Leica is going to have a problem having customers chase their digital cameras with a price range of $5K to $10K. And with the dollar dropping in value there is no telling how high these prices will go. If you want to stay in the Leica game, you may have to go back to shooting film, especially if you already have all of the great Leica M lenses. The new M10, which Leica is working on now will probably be a $10K camera. Too much money for most people to pay for a soon-to-be obsolete camera. My Leica film cameras will never be obsolete as long as someone is still making 35mm film. My M lenses have already appreciated at least 30% since I bought them. I’m keeping the great ones that I have and not buying anymore. Get a couple of M cameras and shoot film. If you do, you can stop chasing rainbows.
No other camera maker is willing to go into the expensive (R&D – low numbers – low revenue – niche) full-frame compact market. If you’ve got your range of beautiful Leica lenses already, and want to use them at their true focal lengths, Leica will always be the only option. Digital if you’ve got the cash, film for everyone else. I’m not in their $10k+ target group either, so I will stick to film as the poor man’s full-frame option. Just bought a M4-P and love it a lot.
I, like Steve I think, am a sucker for a new camera. However, I agree with Rick that we should, perhaps, stop chasing rainbows. The continual “improvement” of digital cameras is beginning to tire me out. We should all look at our current set-ups and ask ourselves “Am I getting great photographs?” If the answer is yes, we should consider ourselves satisfied. If the answer is no, we should then go on to ask “Is the problem the camera or my technique?” I would argue that in the majority of cases, including my own, the latter would be the honest answer. Viewing 100% crops is not how photographs were meant to be appreciated…who did this in the days of film? Let’s break the stranglehold of the manufacturers and simply enjoy the equipment we have, using it to produce great photographs. I really hope that I can do this myself. I am currently having my head turned by the fuji x10, a beautiful looking camera. Will it produce hugely superior photographs (printed at A4) to my olympus xz1 ? Most likely not. Different but not better. I have, therefore, resolved to stick to my xz1 and get the best out of it until it gives up the ghost. i am now looking forward to spending many years getting to know it better and using it as a trusted tool to make photographs.
With help, I can kick this wicked (-ly expensive) habit and enjoy my photography again like I did in the days of film when I had my OM10 for 15 years!
Having said that, I’m really looking forward to Steve’s review of the NEX 7….AArrghh! I’m slipping already.
+1
Disclosure : I shoot with an M9 and an M3 (plus a load of other stuff but day to day the M9 is my go to camera). I can’t see why I would buy an M10. What will it do extra – make me tea and toast in the morning? Those of us who think the M9 IQ is superb shouldn’t need to by a 10. I use Leica because the lenses are stunning. That’s it. Coupled with either my 3 or 9 I get great results. No need to lay down $10k for a 10. I do have other lenses but they tend to be specialist stuff – an 800mm Canon prime for birds for example. I love my 24 ‘lux and my Nocti. Where Leica will lose me is if someone can produce a Nocti 10x cheaper. Fingers crossed.
+1.
People want Leicas because they are expensive. It’s an aspirational luxury brand — a Veblen good (google it), like a Patek Phillipe.
Have you noticed that they can’t meet the demand already for their $5-10k lenses and their $8-$26k cameras? That indicates that their pricing is perfect. If anything, they can and should raise prices — just not before I buy one.
One thing that the NEX can not do better – is to use the full potential of the character of the lens – as large pert is cropped away. To my eyes the NEX produces more pleasing color. Detail wise the NEX seems indeed over-sharpened (looks like Unsharp Mask with large radius). The M9 output is less bitting but somehow more natural – less ‘digital-like’ (for the lack of better word).
The CA with NEX is very strong and indeed it is mostly lens induced (even though digital sensors seem to put put more CA than we see on film). I am quite sure that the M9 does in camera correction – there are good reasons why the Leica lenses are coded and have profiles assigned. Look at the first two images – the CA in the out-of-focus areas is about the same for both NEX and M9.
But yes – the NEX looks like a camera one could use 🙂
M9 does not do any CA correction. CA comes mostly from sensor bloom by using fast glass in high contrast situations. The 6-bit coding is to tell the camera what lens is being used and to apply the corner fix to wide lenses. Thats about it. If I turn off lens coding you will still see the same amount of CA.
OK, I see. Thank you for the explanation. I guess I need to read a bit more on the topic.
Awesome work. I can’t wait for NEX 7. Could you post the raw of M9 and NEX 5N for download? Phase One C1 6.3 has preliminary support for NEX 5N and 7. Thanks!
There is no rational reason to purchase a Leica.
Buy one if you like it. End of story.
apart from snobery that is
I find Nikon and Canon owners to be far bigger snobs.. or perhaps they come off that way from often being oblivious to the fact that there are other makes besides Canon or Nikon. ‘If I’ve not heard of it, it must be rubbish’ mentality. Same as car brand snobs.
Here’s another thing I’ve noticed:
On a close inspection of your mom’s jeans, I can see the M9 retains the fabric’s detail better (the jeans has a diagonal weave). The NEX-5N turns it into a total mess.
This is probably due to the following:
1. Over-sharpening by the NEX-5N
2. Larger sensor on the M9, that can retain small details better.
[img=http://www3.picturepush.com/photo/a/6514406/640/6514406.jpg]
While I agree that in this picture M9 has has rendered the fabric much better it is caused mostly by slightly different focus point in case of the 2 cameras (her fingers are also a lot less sharp in the case of 5n, while face seems similar) and by the fact that M9 does not have the AA filter. Off course it also seems that you are correct that the sharpening radius is a bit too large for 5n.
Thanks, Andy.
I forgot to mention that the M9 doesn’t have an AA filter, which is a good thing. Fine details are preserved much better without an Anti-Aliasing filter.
I wondered, though, how Leica managed to get by without an AA filter and still use a Bayer-pattern sensor? I assumed that diagonals would look terrible without some sort of smoothing, and the Moire problem might appear. After digging-around a little, I found out that Leica has chosen to deal with any possible Moire using in-camera DSP. This approach is evidently better than using an AA filter.
Hi Steve,
Thanks for posting those OoC comparison photos. Been looking forward for this M9 vs NEX-5N.
I have a few comments, now that I’ve examined the photos at 100%:
1. NEX-5N greens lean more towards yellows (can be easily fixed in ACR / LR to make it look more like the M9). Overall, NEX-5N seems slightly more redish.
2. NEX-5N sharpening was stronger. Maybe you should have set sharpening to -2, to make it more like the M9’s default sharpening.
3. NEX-5N seems to have a bit more dynamic range in the shadows (if both photos of the door were exposed the same).
But on the other hand, the M9 seems to have stronger blacks. The NEX-5N blacks can be easily fixed in ACR / LR to have the same blacks on the expense of DR. Also, there’s seems to be a bit of camera shake on the NEX-5N photo of the door.
4. In the photo of your mom standing on the path – the M9 seems to have a warmer tone overall, making her white jacket look very neutral, as should be. That jacket looks a little bluish on the NEX-5N. This seems like the cameras chose different WB temp. The NEX-5N engine must have assesed a different area of the image in order to determine the WB.
There’s CA around your mom’s left arm in the NEX-5N, yet no CA at all on the M9. Same glass, yet different results…Interesting.
5. You did not mention in which mode you shot the JPEGs of the NEX-5N. Portrait? Landscape? something else?
By the way, I own the NEX-5, and from my experience – Portrait gives the most dynamic range. So I always set the camera to Portrait. Can you tell us if the NEX-5N has more DR than the previous NEX-5? I know you don’t have the NEX-5 anymore, but if you take a similar photo with the NEX-5N and let us see the side-by-side, it would be very helpful.
For me, dynamic range is very important. Extracting details out of the highlights and shadows is something I’ve gotten quite good at…but the DR the camera can record is the limiting factor. I sure hope the NEX-5N has a +1 stop more than the NEX-5.
Interestingly -while it’s true, the purple fringing is bad- the colour from the Sony is more accurate. Take the sandstone as an example: the M9 colour is WAY too blue. It’s completely wrong.
With that lens on that body -ringing in at well over ten thousand dollars- this is an absolute joke.
Not a real comparo unless it’s blinded.
Thanks, Steve … Your crazy comparisons really give you a unique perspective on equipment that goes beyond all the technical babble — keep ’em coming!
I don’t currently own any Leica gear but after a great experience renting a M9 and a couple of lenses for a long weekend I’ve about convinced myself to spend some serious cash. Perhaps with a NEX 7 I can start my investment with a good Leica lens and save my pennies until the M10 (or whatever it’s going to be called) is released.
good comparison, powerfull giving. tks very much.
hope more and more comparison will be come out.
Both cameras gave kinda weak results. Sony has good justification though – it’s cheap, but Leica lately is a big disappointment. I don’t see excuses to buy Leica other than the same reason that makes people buy luis vuitton bags – irrational motive.
Well… Seems you never used a M9.
I’ve used a 5D II which is supposed to be the best full frame DSL out there, one year long… And went right back to the M9. The CCD sensor gives incredible results in terms of color and contrast rendition. There is far more to a picture than sharpness (which about any modern camera can give you)…
Thanks for the fun comparison, Steve! But it’s only a fun comparison, indeed. If I would have to pick a winner, I couldn’t, some pictures look better with the Nex, some with the M9P. I like the contrastier outputs of the Nex though, but yeah, it all comes down to JPEG processing, anyway.
People really don’t have to worry about comparisons like these, because you don’t pay your 6000€ for the best digital camera, but just for the only full frame digital rangefinder. Plus, it’s a Leica and handcrafted here in Germany, so it’s worth the money I guess. It might not have the best sensors of all time, neither the best JPEG processing, but we shoot RAW anyway, don’t we?
What I find funny is that the Nex in some way is truer to Oskar Barnack’s ideal of maximum portability than the bulkier M9P 😀
A last thought: if I would have started photography with a rangefinder it would give me the ultimate shooting experience, too, I guess. But since I started photography with an electronic viewfinder (Sony a55), the Nex 7 will always be a better camera for me than any Leica (at least in principle). I have my Leica film rangefinder and it’s a pleasure to use, but if you really think about it, good EVFs are just superior to any other finder system, IMHO.
Thanks. too much choice for me. The little voice in me says the M9 is too expensive for what it is and I am paying for the initial R&D rather than for cost of the components.
I will stick to Slide film.
Steve,
How do you go focus with the Nex5n with the leica lens. Is it automatic, and if manual how does it work?.
I am thinking of getting the Upcoming sony NEX-7 for the missus and to use my 35 cron on it, but she cant handle the RF focus style, so I was wondering?
Steve
Thanks for the comparison. I think the NEX-5n is giving the M9 a good run for the JPG. I think most of the images are well done and there are noticable differences, but I think they may be less than we think. Comcerning CA, or purple fringing, in the first pair of images there is a fair amount of camera shake in both images (up & down for the M9 and side to side for the 5n), which is probably what the “finging” is. In the 2 images of your Mom, I think the 5n may have a slight amount of focus shift from the M9, which would cause the halo effect around her shoulders; this may also be camera shake.
Keep up the good work. I am looking forward to the raw comparison.
PaulB
I’ll disagree for the fun of it. If you zoom in on the shot of the woman, the NEX5N shows crazy CA (already discussed above), less detail and even some artifacting in the woman’s hair, as well as noticeable over-sharpening (it’s actually quite shocking if you rapidly A/B the images). Given that jpegs should be a strong point for Sony, and are a known weakness for the M9, this is disappointing. I also much prefer the way the woman’s skin is rendered in the top image: it has that characteristic Leica glow I recognize from shooting film with my M6.
Hopefully this is just the way the Sony handles jpegs. Similar issues with over-sharpening, CA and even noise (surprisingly) can be seen in the other images.
Don’t get me wrong, I’d like a $700 mini-digital Leica as much as the next person. However to my eye, the Nex5N shot of the woman looks great, but it doesn’t look particularly Leica-like, which to me is the (only) point to shooting these lenses on a digital body.
Anyway, I hope the RAW files will be a different story. As I said, I’d love for this to be an inexpensive/high IQ body for my so-called “legacy” glass. I’m certainly not about to afford a M9.
I’m with you. The NEX images do not impress. The level of CA is attrocious. And finer details are blurred beyond recognition. Just look the last set of images at 100%. The detail in the weatherboards and brickwork is stunning with the M9. The NEX has just muddied all the texture in these materials. The M9 is not reputed to have a strong JPG engine but it is still streets ahead of the NEX. You get what you pay for.
Jpegs should be, but they are not a strong point with Sony,
With the NEX there is no reason to use their lossy inefficient JPEG at all, as their raw files are less than half the size of the M9 are far more widely(computer performance wise) to process.
Still as much as it makes me cringe: I stick to DNG on my M9. After 9,500+ actuations I’ve yet to shoot a single Jpeg with it even though the 45-50mb DNG files are very unwieldy to process even on a workstation… well until adobe gets their head out of their rear and gives genuine multi core use on all aspects of their programs.
BTW, sucks about that stuck red pixel on his M9-P 🙁
Apples and Oranges (M9 vs. Nex)?
It could very well be. I remember when I tested the M9 3 times and compared actual prints (Epson Exhibition Fiber 17″x22″) side by side with my M8 and I could not tell them apart. I felt the M9 was a little bit better than the M8 but not that much. Now we have the NEX 5n and the soon to come NEX 7. Judging from what I am seeing, and from this comparison by Steve, I see very little difference between the M9 and the NEX in terms of picture quality.
The question is what do we get in the M9 for the extra $6,000.00 or so other than a different layout, a true rangefinder, full frame, and extra heavy German build quality? Given the technology changes every year, the case can be made the Sony makes more sense. Why buy a digital camera whose metal shell and rangefinder will outlast the outdated technology it will have inside? In some way, the M8 upgrade program “Camera for Life” made more sense. Why throw away the good body shell and rangefinder when all that is outdated are a chip and circuit boards? In some ways, it is too bad Leica did not take a modular approach to the digital M where upgrades could have been done in a snap, and your body shell and rangefinder would be good to go for decades.
Well, I currently use 2 M8 cameras, and I plan to purchase the Nex 7 as my next Digital M mount camera. Will I ever buy an M9? Maybe in a few years when they come down to $2,000 (by then, the M8 should be under $1000 – this is called digital rot) and only for the reason to have the rangefinder experience. By that time, we will have a NEX full fame, maybe a Fuji Full frame, Zeiss, etc,,,, in the $2000 range with superior performance. By that time, $2,000 for a used M9 would be the correct price, and honestly, even today, I would not pay more than $2000 for one.
its call the GXR.
Optimism: that’s a good one! LOL.
I must say that like the older NEX3 the NEX 5n sure loves its balance on the warm side. Still there are many many improvements, specifically the Offset lenses for wide angle RF lens use that makes me wonder why any sane person would bother with a GXR; whose outdated sensor module cost more than the whole camera should, or even worse, M43 for RF glass.
Thanks Steve , from what i saw i think there is a great difference between the two systems ,despite resolutions , sharpness ,ca … , i think it is a deference between two worlds , the Leica world with its long film history and Sony with its video and digital history , both have a completely different taste , for me it is Leica with this film like feeling, it is magical and incomparable to any modern digital system . i wish Leica keep headed in that direction in there forthcoming products and not tempted by this superior digital specification race.
I hope that your comment was ironic
Agree with Barky.
As for the sample photos – it is subjective, as it should be, but
the Leica’s look much nicer to me.
I’ll say what you can’t. Except for the picture of the mausoleum & the shack in which the 5N is slightly front-focused, the 5N walks all over the M9.
Honestly, I have nothing against the M9 which was a great camera a few years ago when it first came out, but today I’d take a 5N over the M9 even if they cost the same.
Not only is the image quality better but you get — magnified view focusing; the ability to use close focusing lenses, even macro; the ability to use longer lenses; the ability to use great cheap non-m mount lenses; etc.
Totally agree, it is quite obvious that Nex 5n output is at least of the same quality as m9 and to defend 10x higher price with the rf exeprience, feel and what not and say that nex 5n feels like toy is just, well, I’ll be genereous-preposterus. It is surely image quality that should matter for the people who have passion for photography and not to use them as fashion items.
I think that the fact that couple of comparisons shots were of the graveyard tombstones is nice metafor for the M9…
And in other news, Rolex watches tell the same time as Timex watches…
sounds like the M9 isn’t in your market Mika. Good for you.
well, that timex/rolex or mass produced/hand crafted dichotomy for something that was originally desgined for its function and not as an aesthetic object began when watches started to be fashion accessories and status simbols and not devices that tell time. Thanks for confiriming what I said, in accordance to your metaphor/comparison Leica is more fashion accesory than device for producing art/taking photos. Thats fine that people are buying them for what they are but then they should just admit that instead of repeating cheap I am buying soul etc. marketing slogans.
It’s the smallest full frame digital camera. That’s what I wanted. It takes great pictures too. So, it’s more than a fashion piece but there are plenty of cheaper great cameras. To pay that much just because one thinks it takes better pictures is crazy. I also wanted a rangefinder and that was important to me, so this was the only option. I couldn’t care less if it said Leica or Sony. No one even knows what kind of camera I have so it’s not snobbery for me! I think I’ll buy a NEX too!
Sorry, Steve – but with your experience with the M9 you should know that shooting the M9 in JPG is like… well (beware: stupid car comparison) buying a Porsche and putting Fiesta tires on it.
http://dl.dropbox.com/u/15845231/L1034522web.jpg
This is what you get *easily* out of an M9 with 50 Summilux (f/5.6) with LR3 and minor sharpening and it will send the NEX’ results to oblivion anytime.
It’s interesting what you said about the 50L – I had comparable experience with my copy. Canon couldn’t fix the (huuuge) front-focus at distances >5m, so I changed completely to Leica and haven’t looked back 🙂
I have MANY M9 RAW files and yes, the M9 puts out some amazing quality with the RAW file, but maybe the 5n does as well? Don’t know yet because I have not yet processed a raw file from the 5n. As soon as I can, I will. Thx
Thanks for the response. Of course you have 🙂 I was just curious, why posting M9-Files in JPG. That’s just gonna make people think “mhh, well – the Sony’s really sharper” and they’ll call the Leica an overrated and especially over*priced*. Not that I care as I’m happy, but that’s not (entirely :D) true.
The Leica still has the best image quality of all full frame digital bodys (at lower ISO of course), just matched by the new APS-sized Sigma SD1. There might a lot other cameras delivering images that look sharp – but an image from e.g. the 50 Lux and an RAW processed M9-File will give you the next step, it just looks a lot more plastic. And basically all of that feel (and advantage) is lost when shooting the M9 in JPG 🙁
I sure would be happy to see a RAW-comparison. Keep up the good work, it’s always a pleasure to step by and lean back for some minutes 🙂
the m9 cannot be compared to the sd1. the sd1 image quality and sensor at the moment is way ahead. If the nex DR can beat the M9 as u can see here, the SD1 will outresolve M9 like (beware:stupid car comparison) ferrari vs honda jazz
Do you mind sharing please what was your focus point, what was your distance to it and what is approximate size of that house?
A pretty normal sized house 😀 I think it’s about 20m and i focussed in the middle (at the edge of the windows)
Off topic
Short question i’m not going to buy a leica m9, i already have a GF1, with some lenses, but i will like to have something better, what is my best option today a Fujix100 ?? or a Sony N7 o N5 ?? i hate the toy filling. In fact i will like a camera like a leica or Contax G2 or a Pentax Mx
Greg
I’s sorry for asking this here, there is no more forum !
Id go with a Fuji X100 or wait for the NX-7 which may feel better than the 5n in the hand. The 5n doesn’t feel like a camera, mores like a gadget but the 7 may feel more like a traditional camera with its larger size, knobs and built in VF.
Steve speaking of another camera really quick, a while ago you posted a video about the Leica CL, and I can’t find the review.
Did you dislike the camera enough to not post a full review? My primary camera which is an M6 sees much silver-halide running through its veins, but I’ve always been interested in a small CL as a secondary camera, and in some cases as a stealthy primary shooter because of its size. I’ve also heard that the 40mm Summicron is outstanding! If you have time to reply I would be grateful.
Thanks again
I loved the CL but the meters break down in them easily so it’s tough to recommend if you want a meter. Ive seen about 7 CL’s with busted meters in the last two years. Id stick with the M6.
I’ve got the Leica CL as well as small pocket camera and I love it a lot. As steve said you have to make sure the lightmeter is ok, but mine is and gives a good reading. The 40mm summicron f/2 is a great lens that’s cheap too.
I agree that the CL is a nice camera. I bought a used one in the ’70s, and while it developed meter issues (linearity and “sticky” needle when turned on), it’s been perfect again since Gus Lazzari restored it over a year ago. I’ve also had M Leica’s since the ’60s, but the CL is a great carry-around camera. Find one with a good meter, or get Gus to fix it.
Based on what I like about the CL I also bought its big-brother, the M5. It’s the most under-rated Leica around!
Thanks for all of the comments and advice!
Good to see Sony setting the bar high for Leica’s upcoming evil camera next year. Especially the nex-7 will be the camera to keep their eyes at and to beat. I think Leica can only make it work, and surpass the competition, with a full frame sensor now. Which might directly compete with the M9+series then. Oh dilemmas… 🙂
I’m wondering if the Sony Nex 5n has the same/similar sensor to the very nice sensor in the Pentax K-5. One of the few critiques that people of have had of the K-5’s sensor is an increased incidence of purple fringing for some lenses, especially lenses that were not designed for digital.
(note: The K-5’s sensor is 16 mp CMOS and also made by Sony.)
From what I’ve gathered K5, Nikon D7000, Sony a580, a55 and nexc3 all have the same sensor and the sensor in 5N is similar but slightly tweaked (whatever that might mean)
The 5N sensor is a new 16.1mp APSC sensor capable of producing 1080P 60 fps per second, and delivering 10 full resolution frames per second for stills. The previous Sony 16.3mp APSC sensor as used in the K5, Nikon D7000, Sony a580, a55 and nexc3 was only capable of 1080i video. Besides thespeed improvements, it looks appears High ISO performance has also improved by about a stop with the new sensor as well. Lots of exciting things are yet to come from this new 16mp sensor once Nikon and Pentax get to tweak it a bit. It is certainly fantastic in my NEX-5N.
Also, microlenses for better performance in the corners.
Hi Steve,
thank you for comparison. In the introduction you were very detailed about the RF experience etc but there is only one half sentence about the image quality:
“the image output is not that far off at all from the M9”
what do you mean when you say this. I’d be very interested to hear in what aspects is photo quality of M9 better than Nex beacuse I just can’t see it, I actually see it the other way around. I know that Leica is meant to be shot raw but even then I don’t think that it will change much.
Thanks Mika. I like to show the samples I get and let YOU guys be the judge for your own needs and wants. These are all out of cam JPEGS and some will say the NEX shots are better and others will say the M9 are better. The M9 excels with RAW, not so much JPEG. Looks like the NEX excels with JPEG, and should get even better with RAW.
The 5n is better at high ISO of course, but it is still a crop sensor and will not give the same FOV as the M9 with the same lenses. As far as IQ, color, DR…the NEX is clearly holding its own.
Thanks, I’d always rather buy 10x cheaper camera that has at least the same image quality and invest the rest of the money into travel to actually get to use it.
You mentioned while ago that you were testing/planing to test M9 against 5dmkII, did you get time to do that?
I did test the M9 and 50 Noct against the 5DII and 50 L. The 50 L was so awfully bad I couldn’t/wouldn’t post as I assumed the 50L I had was defective. I knew of the focus shift but assumed that the copy that was sent to me was beyond that. The color, contrast, and sharpness was way below the M9.
It must have been bad copy as many people whose work I like are using 50 1.2 without any problems. I never had any experience with it as it is too expensive for me, I use Nikon 50mm 1.2 AIS with adapter on 5D and it is great.
how can there be so much uncontrolled CA out of the Nex?
I believe it is a sensor thing. There is plenty with the M9 as well, and the Noctilux is much worse in this regard. Guessing the 7 will be the same. This always happens with fast glass and high res sensors.
We must be looking at different images. In comparison images #3 and #4, CA in the tree foliage on the right and around the tombstone look downright ugly with the NEX. The M9 shows zero CA in the foliage and minimal CA around the tombstone. As far as I’m concerned the NEX looks like my $100 point and shoot in this regard.
Does the M9 correct things like that in its JPEG outputs? How does it identify the lens it’s using? NEX surely isn’t correcting anything… I don’t know about M9 because I’m not familiar with it at all. Might that be the case?
No the M9 does not do any CA correction.
Looks like it does correct CA in JPEG: http://www.imaging-resource.com/PRODS/M9/M9A4.HTM
Now that you point those two sections out, they are pretty bad on the NEX
Thanks Steve, would love RAW comparisons when the 5N raw is supported!
Steve,
Thank you for the side by side comparison. In my opinion new cameras like the 5N are game changers for Leica. At least before this, one could justify a $10K investment on an M9 + glass believing you were actually getting better image quality … that is clearly not the case anymore.
I have been sooooo ready to plunk down cash on an M9 but will wait now to see where the M9.2 or M10 goes.
Question, I assume the Sony 5N is not full frame – so did you have to take a few steps back to achieve the same image perspective with the same lenses?
It’s actually not exactly the same image perspective/framing ! and I think I kinda prefer the NEX rendering after all… Except on the last one which definitely looks more natural for the leica…
On any of the pictures where I like the Leica better than the Nex, I also see a huge difference in exposure/dynamic range.
For example the last two; I prefer the colour of the Leica, but with the Nex I can actually tell what is in the dark spot on the left side.
What kind of exposure was used?
Doesn’t the converter magnify the shots versus pure Leica? You can see it in the cottage shots. I am a beginner but is this a true comparison then?
Wow, the purple fringing from the Nex5 is out of control.
As you surely know, CA is lens artefact and not camera, the fact that it is seen in nex jpegs means that camera is not doing CA correction.
The M9 does not do any CA correction either. The CA comes from the sensor, not so much the lens though fast glass and high contrast stresses out almost any digital sensor. Any fast lens will produce CA on the M9 or the NEX-5n but you do not see CA on film images because it is a digital sensor issue not a lens issue.
yes, CAs can be present on film images as well, they are caused by a lens having a different refractive index for different wavelengths of light so lens is not focusing different wavelengths of light onto the exact same focal plane, simple physics. Sensor also can play a part so different companies optimize sensors, camera construction etc. for their lenses and therefore you won’t see as much CAs on sony with their newer lenses or on canons and nikons with respective lenses.
True, i shot some 120 film with my mamiya rz 67 and a 180mm and wide open i saw some CA .. film do have CA i confirm
indeed. my eyeglasses produce CA.
Steve, thank you for this comparison, as always great job.
WOW, I noticed my pre-asph 35Lux producing some CA on m4/3, but this one is pretty bad. It would be nice to see how 75APO would have compared in this situation.
I did not do any tests, but just by looking at images I did notice pretty much no CA when using APO 135mm on m4/3, (thats why I love using cine lenses on mirrorless cameras, cause most of the good ones were apo like with super optical correction)
1st thanks for doing the work and posting this information. Looking at both files makes me glad I don’t have either camera as the combination of purple fringing from blooming and Axial CA from the lens looks really bad. A lot of older lenses do exhibit some Axial CA which is purple or green fringing on edges just inside or outside the DOF. Probably the purple along the line of the memorial structure is sensor blooming on both but the purple in the tree leaves near it look more like Axial CA. You could easily test for which is which by varying aperture and exposure. Axial CA will go away with smaller apertures but not blooming. Lower exposure may help with blooming.